

The Moon is the only object near enough that its distance can be found fairly accurately with measurements made without a telescope. To measure their distances requires a very large baseline and highly precise angular measurements. Unfortunately, nearly all astronomical objects are very far away. The farther away an astronomical object lies, the longer the baseline has to be to give us a reasonable chance of making a measurement. In practice, the kinds of baselines surveyors use for measuring distances on Earth are completely useless when we try to gauge distances in space. Thus, we have the general rule that the smaller the parallax, the more distant the object we are measuring must be. If the tree were farther away, the whole triangle would be longer and skinnier, and the parallax angle would be smaller. The solution could be reached by constructing a scale drawing or by using trigonometry to make a numerical calculation. A knowledge of the angles at A and B and the length of the baseline, AB, allows the triangle ABC to be solved for any of its dimensions-say, the distance AC or BC. The parallax is also the angle that lines AC and BC make-in mathematical terms, the angle subtended by the baseline. By getting the angle to a tree from two different vantage points, we can calculate the properties of the triangle they make and thus the distance to the tree.
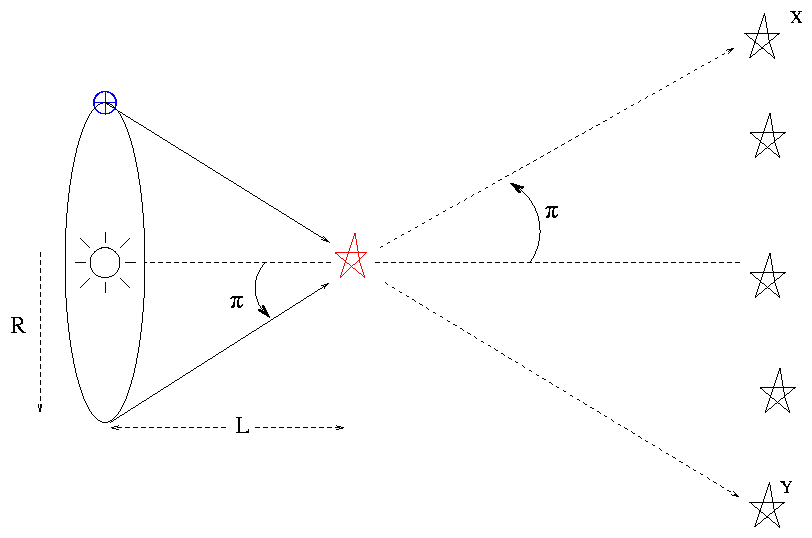
Triangulation allows us to measure distances to inaccessible objects. This apparent change in direction of the remote object due to a change in vantage point of the observer is called parallax.įigure 19.4 Triangulation. Note that C appears in different directions from the two stations. Now the direction to the tree (C in the figure) in relation to the baseline is observed from each station. That distance (line AB in Figure 19.4) is called the baseline. You set up two observing stations some distance apart. Suppose you are trying to measure the distance to a tree across a deep river ( Figure 19.4). Let’s see how surveyors take advantage of the same idea. In order to see the shift of an object a city block or more from you, your eyes would need to be spread apart a lot farther. This is because our depth perception fails for objects more than a few tens of meters away. If your arms were made of rubber, you could stretch the pen far enough away from your eyes that the shift would become imperceptible. Your brain automatically performs such comparisons and gives you a pretty good sense of how far away things in your immediate neighborhood are. If you play with moving the pen for a while, you will notice that the farther away you hold it, the less it seems to shift. Now hold the pen at arm’s length: the shift is less. Note how the pen seems to shift relative to objects across the room. Look at it first with one eye (closing the other) and then switch eyes. To see what we mean, take a pen and hold it a few inches in front of your face. You therefore view the world from two different vantage points, and it is this dual perspective that allows you to get a general sense of how far away objects are. As you are pleased to discover every morning when you look in the mirror, your two eyes are located some distance apart. Triangulation in SpaceĪ practical example of triangulation is your own depth perception. Even so, we can, in principle, survey distances to the stars using the same technique that a civil engineer employs to survey the distance to an inaccessible mountain or tree-the method of triangulation. 1 The nearest star, however, is hundreds of thousands of AU from Earth.
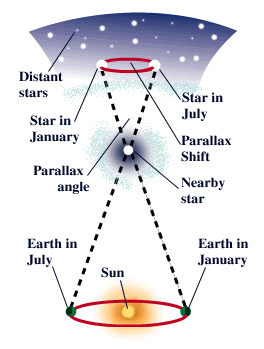
As of 2021, Voyager 1 is 152 AU from the Sun. For example, our Voyager 1 probe, which was launched in 1977, has now traveled farther from Earth than any other spacecraft. It is an enormous step to go from the planets to the stars. Discuss astronomers’ efforts to determine the distance of the stars closest to the Sun.Explain why space-based satellites deliver more precise distances than ground-based methods.Understand the concept of triangulating distances to distant objects, including stars.By the end of this section, you will be able to:


 0 kommentar(er)
0 kommentar(er)
